Расчет скалярного произведения с использованием Numpy в Python
Last updated
Last updated
В этом учебнике вы научитесь использовать Numpy для расчета скалярного произведения в Python. Знание того, как понимать и вычислять скалярное произведение между скалярами и векторами, является важным навыком в машинном обучении. Этот пост подробно расскажет о том, что такое скалярное произведение и как его вычислить. Вы научитесь вычислять скалярное произведение между двумя одномерными массивами, одномерным массивом и скаляром, а также двумя двумерными массивами.
Быстрый ответ: используйте numpy.dot().
Оглавление
Скалярное произведение, или точечное произведение, берет два вектора равной длины и возвращает скаляр. Скалярное произведение алгебраически выглядит так:
s = x ⋅ y
где: s - это скалярное произведение двух векторов, а x и y - два вектора.
Это можно представить как:
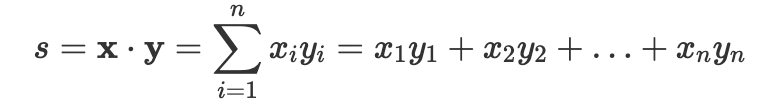
Этот учебник исследует три различных сценария скалярного произведения:
Скалярное произведение между одномерным массивом и скаляром: возвращает одномерный массив
Скалярное произведение двух одномерных массивов: возвращает скаляр d
Скалярное произведение между двумя двумерными массивами: возвращает одномерный массив
Давайте изучим, как использовать Python для вычисления скалярного произведения между одномерным массивом и скаляром.
Проверьте другие учебные материалы по Python на datagy, включая наше полное руководство по стилизации Pandas и наш исчерпывающий обзор сводных таблиц в Pandas
numpy, популярная библиотека Python для науки о данных, содержит множество полезных функций работы с массивами. Одна из этих функций, dot(), может быть использована для вычисления скалярного произведения в различных сценариях, как вы узнаете в этом руководстве.
Функция dot() используется как для вычисления скалярного произведения, так и для умножения матриц, в зависимости от типов массивов и скаляров, переданных в функцию.
Давайте посмотрим, как выглядит функция:
В приведенном выше коде мы сначала импортировали numpy с использованием псевдонима np. Затем мы можем получить доступ к функции dot(), которая принимает два обязательных параметра: x и y
Зависимо от типов данных, переданных в аргументах, будут выполняться различные вычисления - либо скалярное произведение, либо умножение матриц.
В следующем разделе вы узнаете, как использовать numpy в Python для вычисления скалярного произведения одномерного массива и скаляра.
Хотите научиться вычислять и использовать натуральный логарифм в Python. Посмотрите мой учебник здесь, который научит вас всему, что вам нужно знать о том, как это сделать в Python.
При вычислении скалярного произведения между одномерным массивом и скалярной величиной вы, по сути, умножаете каждый элемент массива на скаляр.
Давайте рассмотрим пример. Вам дан одномерный массив [1, 2, 3] и скаляр 2. При расчете скалярного произведения между этими двумя значениями вы умножаете каждое значение в массиве на скаляр.
Тогда это выглядит так:[1x2, 2x2, 3x2].
переводится как `[1х2, 2х2, 3х2]
Теперь, когда мы поняли, как выглядит скалярное произведение одномерного вектора на скаляр, давайте посмотрим, как мы можем использовать Python и numpy для расчета скалярного произведения:
Мы можем увидеть, как легко numpy позволяет рассчитать скалярное произведение между скаляром и вектором. Давайте разберемся, что мы здесь сделали:
Мы инициализируем две переменные: x, которая представляет скаляр, и y, которая представляет массив numpy.
Мы затем рассчитываем скалярное произведение между двумя векторами, используя функцию np.dot()
При выводе результата на печать мы видим, что он представляет собой одномерный массив, содержащий произведение каждого значения исходного массива на скаляр.
В следующем разделе вы научитесь вычислять скалярное произведение двух одномерных массивов, используя Python и numpy.
При вычислении скалярного произведения между двумя одномерными массивами возвращается скалярное значение. Этот расчет выполняется путем суммирования произведения значений в каждом из двух массивов.
Из-за этого массивы должны быть одинакового размера, иначе точечное произведение не может быть вычислено.
Давайте рассмотрим расчет скалярного произведения между двумя массивами [2, 4, 6] и `[3, 5, 7]
При вычислении скалярного произведения двух одномерных векторов мы вычисляем умножение первого вектора на транспонированный второй.
Для этого мы вычисляем следующее: [2 x 3 + 4 x 5 + 6 x 7], что упрощается до [6 + 20 + 42] и возвращает скалярное значение 68.
Давайте посмотрим, как мы можем вычислить скалярное произведение двух одномерных векторов с использованием numpy в Python:
В следующем разделе вы узнаете, как вычислить скалярное произведение между двумя двумерными массивами.
При вычислении скалярного произведения между двумя двумерными массивами возвращается двумерный массив. Это достигается за счет умножения матриц друг на друга.
Рассмотрим пример с двумя массивами: [[1,2,3], [4,5,6]] и [[4,5,6], [7,8,9]]. Это действительно возвращает массив размером 2x2. Это потому, что скалярное произведение двух двумерных массивов всегда возвращает матрицу размером с количество строк первой матрицы и количество столбцов второй матрицы.
Из-за этого размер первой матрицы должен быть равен размеру транспонированной второй матрицы
Ниже показано, как будет происходить этот расчет:
Теперь, когда мы поняли, как будут умножаться матрицы, давайте посмотрим, как мы можем использовать Python и numpy для расчета скалярного произведения.
Давайте рассмотрим, что мы здесь сделали:
Мы загрузили наши два массива numpy
Мы затем применили функцию np.dot(), передавая в неё первую матрицу и транспонированную вторую.
В следующем разделе вы научитесь использовать оператор @ в Python для вычисления скалярного произведения массивов numpy.
Нужно проверить, существует ли ключ в словаре Python? Ознакомьтесь с этим руководством, в котором рассказывается о пяти различных способах проверки наличия ключа в словаре Python, включая способ возврата значения по умолчанию.
Начиная с Python 3.5+, появился оператор, который позволяет вычислять скалярное произведение между двумя массивами, оператор @. Данный оператор использует различные библиотеки, такие как numpy, для поддержки вычисления скалярного произведения.
Хотя этот подход все еще использует numpy, он может помочь упростить процесс вычисления скалярного произведения. Используя оператор, мы упрощаем подход и делаем его более синтаксически ориентированным.
Вместо использования функции np.dot(), мы можем использовать оператор @, как это было сделано в приведённом выше примере.
Хотите научиться получать расширение файла в Python? Этот учебник научит вас использовать библиотеки os и pathlib для этого!
Давайте посмотрим, как мы можем воспроизвести наш пример вычисления скалярного произведения между скаляром и одномерным массивом с использованием оператора @
В следующем разделе вы научитесь использовать оператор @ для расчёта скалярного произведения двух двумерных массивов в Python.
Хотите научиться использовать функцию zip() в Python для итерации по двум спискам? В этом учебнике вам точно расскажут, что делает функция zip() и покажут несколько творческих способов использования функции.
Теперь давайте посмотрим, как мы можем использовать оператор @, чтобы вычислить скалярное произведение между двумя двумерными массивами.
Мы можем видеть здесь, что это возвращает тот же результат.
Нужно автоматизировать переименование файлов? Ознакомьтесь с этим подробным руководством по использованию pathlib для переименования файлов. Если вы лучше воспринимаете информацию на слух, весь учебник также доступен в виде видео в посте!
В этом учебнике вы научились вычислять скалярное произведение в Python. Вы узнали, что представляет собой скалярное произведение, и три различных случая, в которых может быть рассчитано скалярное произведение: между скаляром и массивом, между двумя одномерными массивами и между двумя двумерными массивами.
Вы научились использовать функцию dot() в numpy, а также оператор @, доступный в Python 3.5.
Чтобы узнать больше о функции dot() в numpy, ознакомьтесь с официальной документацией здесь.
