Функция активации ReLU для глубокого обучения: полное руководство по выпрямленному линейному блоку
PreviousNumpyNextКак нормализовать массивы NumPy (минимальное-максимальное масштабирование, Z-оценка, L2)
Last updated
Last updated
В мире глубокого обучения функции активации придают жизнь нейронным сетям, внося в них нелинейность, что позволяет им учиться сложным закономерностям. Функция активации Rectified Linear Unit (ReLU) является краеугольным камнем, обеспечивая простоту и эффективность нейронов за счет снижения влияния проблемы исчезающего градиента.
В этом полном руководстве по функции активации ReLU вы узнаете все, что вам нужно знать об этой простой, но мощной функции. К концу этого учебника вы узнаете следующее:
Что такое функция активации в контексте глубокого обучения
Как работает функция ReLU и почему она важна в мире глубокого обучения
Как реализовать функцию ReLU в Python с помощью NumPy и PyTorch
Какие есть альтернативы функции активации ReLU и когда их использовать
Как решать распространенные проблемы, возникающие при использовании функции активации ReLU
Оглавление
В области глубокого обучения, функции активации формируют процесс обучения, внося нелинейность в сеть, что позволяет ей изучать сложные паттерны и взаимосвязи в данных. В этом разделе мы рассмотрим основные концепции функций активации и почему они так важны для глубокого обучения.
В его основе, нейронная сеть представляет собой серию взаимосвязанных узлов и нейронов, каждому из которых присваивается вес, определяющий его значимость в процессе принятия решений. Суммируются взвешенные входные данные, и результаты передаются через функцию активации, которая определяет, активируются нейроны или нет
Без использования этих функций активации вся нейронная сеть была бы просто линейной моделью, совершенно неспособной захватывать сложные, нелинейные закономерности, присутствующие в реальных данных. Существует множество различных функций активации, в том числе гиперболический тангенс (Tanh) и функция активации softmax, в зависимости от конкретного случая использования, который вы надеетесь решить.
Функции активации в глубоком обучении облегчают следующее:
Изучайте сложные закономерности. Нелинейность позволяет нейронным сетям изучать более важные закономерности в данных, уступая место таким задачам, как распознавание изображений, обработка естественного языка и многое, многое другое.
Градиентный поток: функции активации позволяют градиентам сети течь во время обратного распространения ошибки, что помогает процессу оптимизации.
Граница решения: функции активации устанавливают границу решения в задачах классификации, которая позволяет вашей модели определить, к какому классу или категории принадлежат входные данные.
Теперь, когда у вас есть твердое понимание того, почему функции активации имеют значение, давайте перейдем к тому, почему вы здесь - к функции активации rectified linear unit, или ReLU.
Прямоугольная Линейная Единица, или ReLU, является одной из многих функций активации, доступных вам для глубокого обучения. То, что выделяет функцию активации ReLU, так это ее простота при этом оставаясь невероятно мощной функцией.
Хотя название функции "выпрямленная линейная единица" может звучать сложно, сама функция предельно проста. В своей основе, функция ReLU применяет очень простое правило: если входное значение больше нуля, оно оставляет его без изменений; в противном случае, оно устанавливает его в ноль.
Давайте быстро посмотрим, как выглядит функция:
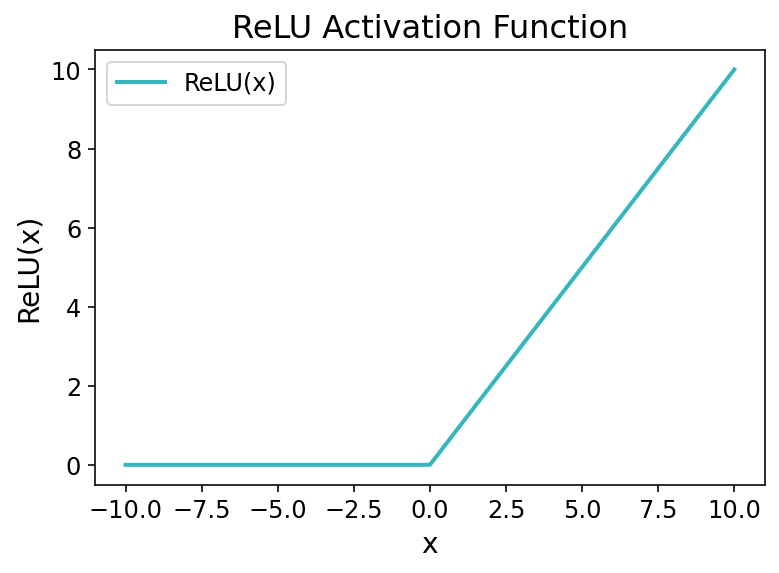
На представленном выше графике вы обнаружите резкий изгиб при x = 0, когда функция переходит от нулевого значения к линейному росту на положительных значениях. Именно это изменение позволяет вашей модели глубокого обучения выявлять нелинейные закономерности, обучаясь сложным зависимостям в ваших данных.
Функция ReLU может быть определена следующим образом:
Функция принимает единственный аргумент x и возвращает максимум из 0 или самого значения. Это означает, что функция ReLU вводит нелинейность в нашу сеть, позволяя значениям больше нуля проходить через нее без изменений, в то время как все отрицательные значения превращаются в нули.
Let’s now dive into understanding the many benefits that the ReLU function provides for deep learning projects.
Выбор подходящей функции активации для проектов глубокого обучения является критически важным решением. Со временем функция Rectified Linear Unit (или ReLU) стала одним из предпочтительных выборов во многих архитектурах нейронных сетей.
В этом разделе мы рассмотрим, почему функция ReLU является предпочтительной функцией для многих проектов глубокого обучения.
Одним из основных преимуществ функции ReLU является её крайняя простота. Эта функция требует очень мало вычислений, что делает её вычислительно эффективной по сравнению с другими, более сложными функциями, такими как функция активации сигмоид
Это позволяет вашим моделям обучаться быстрее, что может быть очень важным фактором при работе с сложными моделями и большими объемами данных.
Проблема исчезающего градиента является обычной трудностью при работе с глубоким обучением. Это происходит, когда функции активации, такие как сигмоид или гиперболический тангенс, создают очень маленькие градиенты для крайних значений, что приводит к медленной сходимости.
Функция активации ReLU помогает уменьшить проблему исчезающего градиента, предоставляя постоянный градиент для положительных входных значений. Когда входное значение положительное, градиент просто равен 1, что означает, что веса могут быть легко обновлены.
Это свойство позволяет вашим моделям обучаться гораздо более эффективно, что может быть критически важно для решения сложных задач.
Функция ReLU способствует разреженности в нейронных сетях, обнуляя отрицательные значения, что означает, что эти нейроны становятся неактивными. Такая разреженность может привести к нескольким преимуществам, например, к эффективности использования памяти, поскольку для их хранения требуется меньше памяти.
Аналогично, нейронная эффективность разреженности может привести к лучшей обобщаемости, поскольку сеть в большей степени сосредотачивается на релевантных признаках и меньше на тех, которые больше влияют на обучение.
Одной из наиболее сложных задач в глубоком обучении является развитие интуиции. Поскольку функция ReLU невероятно проста, она позволяет вашей модели стать немного менее сложной. Она имитирует работу человеческих нейронов, которые активируются, когда пересекается определенный порог.
Это делает функцию ReLU важной при разработке моделей, предназначенных для обучения начинающих или исследователей, желающих лучше понять, как работают нейронные сети.
Вы уже узнали много о функции активации ReLU (rectified linear unit) и о важной роли, которую она играет в глубоком обучении. Давайте теперь более подробно рассмотрим, как мы можем на практике реализовать эту функцию с использованием Python и NumPy. Мы разберем, как определить функцию, и покажем, как использовать ее на массиве данных.
Давайте посмотрим, как мы можем определить функцию активации ReLU с помощью NumPy:
Подобно нашей чистой функции на Python из предыдущего урока туториала, реализация на NumPy использует функцию maximum(), чтобы получить большее из двух чисел: указанного значения или 0. Благодаря тому, что функции NumPy могут работать поэлементно, это означает, что мы можем передать в функцию целый массив значений, а не только одно значение.
Давайте посмотрим, как мы можем использовать эту функцию на практике:
В приведенном выше блоке кода мы сначала определили массив NumPy, содержащий пять чисел, некоторые из которых положительные, а некоторые отрицательные. Затем мы передали этот массив в нашу вновь определенную функцию. Выведя на печать входные и выходные данные, мы можем увидеть, как функция ReLU преобразовала наш исходный массив.
На практике вы часто будете обращаться к функции глубокого обучения для реализации функции ReLU – давайте рассмотрим, как реализовать эту функцию в PyTorch.
PyTorch — чрезвычайно популярная библиотека для глубокого обучения, предоставляющая инструменты для эффективного построения и обучения нейронных сетей. В предыдущем разделе мы рассмотрели, как реализовать функцию активации ReLU на Python с использованием NumPy. В этом разделе мы исследуем, как использовать библиотеку PyTorch для реализации и использования функции ReLU.
PyTorch реализует функцию rectified linear unit (ReLU) с использованием модуля nn. Давайте посмотрим, как мы можем создать эту функцию:
В приведенном выше блоке кода мы сначала импортировали модуль nn, используя стандартный псевдоним nn. Затем мы определили объект функции, создав экземпляр класса nn.ReLU. Теперь мы можем использовать функцию, передавая в нее значения — давайте попробуем:
Давайте разберем, что мы сделали в вышеупомянутом блоке кода:
Мы импортировали как библиотеку torch, так и модуль
Затем мы создали экземпляр функции, как мы делали это ранее
Затем мы создали тензор PyTorch, содержащий значения от -2 до +2.
Затем мы передали этот тензор в объект функции relu и вывели результат на печать.
Мы видим, что значения были правильно преобразованы: все отрицательные значения изменены на ноль, а все положительные значения остались без изменений.
Часто вам может потребоваться реализовать функцию активации ReLU как часть нейронной сети. Давайте посмотрим, как мы можем создать простой класс нейронной сети, чтобы увидеть, как мы можем использовать функцию активации в PyTorch:
В указанном выше блоке кода мы реализовали линейную нейронную сеть и включили в неё функцию активации ReLU. Затем мы создали экземпляр класса и передали в него образец тензора. Давайте посмотрим, как мы можем исследовать эти значения:
В приведенном выше блоке кода мы можем увидеть, как передача тензора данных через линейный слой, а затем активация его с использованием функции ReLU влияет на данные.
Теперь, когда вы научились реализовывать функцию как в NumPy, так и в PyTorch, давайте немного больше узнаем о теории функции ReLU, изучив, как функция решает проблему исчезающего градиента.
Проблема исчезающего градиента является давней проблемой, с которой сталкиваются многие нейронные сети. Проблема исчезающего градиента возникает во время обучения нейронных сетей, особенно при использовании методов оптимизации на основе градиента. Она возникает, когда градиенты функции потерь по отношению к параметрам модели становятся чрезвычайно малыми по мере их обратного распространения через сеть
Это распространенная проблема при использовании таких функций активации, как сигмоидная функция или гиперболический тангенс (Tanh). Эти функции известны тем, что производят малые градиенты, особенно для значений, далеких от нуля. Это приводит к уменьшению градиентов, особенно по мере углубления сетей. В какой-то момент эти обновления весов становятся незначительными, что затрудняет процесс обучения и приводит к медленной сходимости или застою.
Поведение градиентов ReLU, однако, отличается. ReLU обеспечивает постоянный градиент равный 1 для всех положительных значений. Это означает, что в процессе обратного распространения градиенты сохраняют свою величину и способствуют более эффективному обновлению весов. Аналогично, для отрицательных входных значений, ReLU обеспечивает градиент равный 0, что означает, что все отрицательные градиенты просто игнорируются.
Простыми словами, поведение градиента функции ReLU решает проблему исчезающего градиента двумя способами:
Градиенты не уменьшаются экспоненциально: Градиенты ReLU либо равны 1 (для положительных входных данных), либо 0 (для отрицательных входных данных), что гарантирует, что градиенты не исчезают в такой же степени.
Эффективное распространение градиентов: Постоянный градиент 1 для положительных значений позволяет градиентам эффективно распространяться в процессе обратного распространения ошибки. Это позволяет сети более эффективно корректировать веса, ускоряя процесс сходимости.
Однако функция ReLU может сталкиваться с проблемой "умирающего ReLU", когда нейроны в сети застревают в неактивном состоянии и не восстанавливаются во время обучения. Из-за этого были разработаны различные вариации, чтобы решить эти проблемы. Давайте рассмотрим их в следующем разделе.
Этот учебник показал, насколько ценной может быть функция ReLU для глубокого обучения. Однако существует несколько вариаций функции rectified linear unit, которые могут решать определенные задачи и помогать в конкретных случаях. В этом разделе мы рассмотрим некоторые из распространенных вариаций ReLU и обсудим, когда вам может понадобиться их использовать.
Давайте посмотрим, как выглядят эти вариации:
Теперь, когда у вас есть визуальное представление о том, как выглядят эти альтернативы, давайте подробно рассмотрим каждую из них.
Функция Leaky ReLU используется для решения проблемы "умирающего" ReLU, когда нейроны могут стать неактивными и никогда больше не активироваться во время процессов обучения. Она решает эту проблему за счет введения небольшого ненулевого градиента для отрицательных входных значений, что позволяет некоторой информации передаваться через обратное распространение, даже когда входное значение отрицательное.
Давайте рассмотрим математическое определение функции Leaky ReLU:
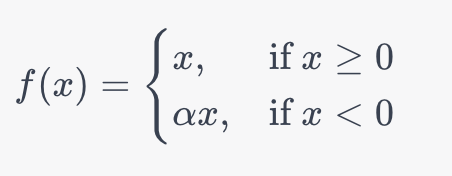
В приведенной выше формуле, α вводит малое положительное константное значение (обычно, в диапазоне от 0.01 до 0.3). Это обеспечивает, что нейроны никогда не становятся неактивными, что позволяет функции избежать проблемы "умирающего" ReLU.
Параметрическая функция ReLU расширяет возможности Leaky ReLU за счёт введения α в качестве параметра, который настраивается в процессе обучения, вместо того чтобы быть фиксированным константом. Это позволяет нейронной сети адаптировать наклон отрицательной стороны функции активации, исходя из конкретной задачи, которую данная функция должна решить.
Давайте рассмотрим математическую функцию, лежащую в основе функции Parametric ReLU:
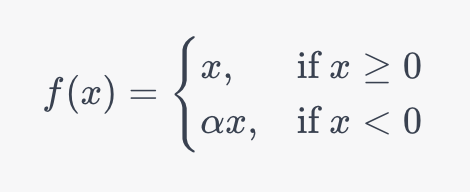
Эта функция чрезвычайно полезна, когда у вас большой набор данных с сильно различающимися характеристиками. Это связано с тем, что функция может обучаться нахождению оптимального угла наклона для отрицательных входных значений, решая проблемы, которые могут возникать даже в функции Leaky ReLU.
Экспоненциальная Линейная Функция (ELU) старается объединить преимущества функций ReLU и Leaky ReLU, добавляя при этом уникальные свойства. Давайте рассмотрим определение функции ELU и исследуем, что делает её уникальной:
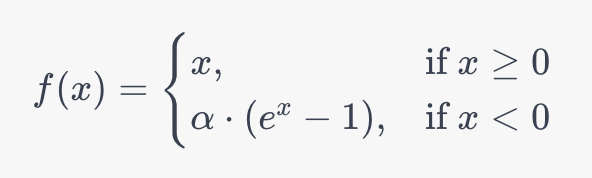
В то время как ELU сохраняет функциональность ReLU для положительных чисел, поведение для отрицательных значений меняется. С отрицательной стороны функции используется экспоненциальная кривая для более гладкой обработки отрицательных входных данных, чем в случае с ReLU или Leaky ReLU. На практике было показано, что это способствует более быстрой сходимости и улучшенной обобщающей способности.
С учетом всех этих вариаций стандартной функции ReLU может показаться сложной задачей понять, когда использовать какую функцию. Ниже приведена таблица, которая разбивает наиболее общие случаи использования для каждой из вариаций функции ReLU:
Стандартный ReLU
Основа для многих сетей, хорошо работает в большинстве случаев.
Leaky ReLU
Используйте, если сталкиваетесь с проблемой "умирающего ReLU" из-за отрицательных входов, которые превращаются в нули.
Параметрический ReLU (PReLU)
Вариант Leaky ReLU, где утечка определяется как параметр, который может быть обучен. Хорошо подходит для задач, где требуется большая гибкость.
ELU (Exponential Linear Unit)
Используйте для ускорения обучения сетей за счет уменьшения эффекта затухания градиентов. Предлагает более плавную функцию, чем ReLU.
SELU (Scaled Exponential Linear Unit)
Автоматически масштабируется в процессе обучения, приводя к самонормализации сети. Используйте в глубоких сетях для улучшения стабильности обучения.
В этом разделе мы изучили вариации функции активации ReLU и определили наилучшие сценарии использования для каждой из них.
Хотя выпрямленный линейный блок (ReLU) и его варианты обеспечивают множество преимуществ по сравнению с другими функциями активации, они также сопряжены с некоторыми собственными проблемами. В этом разделе мы рассмотрим наиболее распространенные проблемы и способы их решения.
Хотя альтернативы функции ReLU решают угасающую проблему ReLU, это может привести к другой проблеме: проблеме взрывающегося градиента. Эта проблема возникает, когда градиенты становятся слишком большими во время обратного распространения ошибки, в результате чего обновления веса становятся слишком большими и дестабилизируют обучение. Для решения этой проблемы можно реализовать следующие решения:
Обрезка градиентов: Сокращая градиенты, если они превышают определенный порог, можно предотвратить их чрезмерное увеличение.
Планирование скорости обучения: Для стабилизации весов можно уменьшать скорость обучения по мере продвижения тренировки.
Выбор подходящего коэффициента обучения имеет ключевое значение для обучения стабильных и эффективных моделей. Это особенно верно при использовании функции активации ReLU из-за её чувствительности к коэффициентам обучения. Это связано с тем, что у ReLU градиенты либо 0, либо 1, что делает её очень чувствительной к коэффициенту обучения. Вы можете решить эту проблему, реализовав следующие решения:
Планирование Скорости Обучения: Этот метод постепенно снижает скорость обучения во время тренировки, начиная с относительно высокой скорости для более быстрой сходимости. Распространенные методы планирования скорости обучения включают ступенчатое уменьшение или экспоненциальное затухание.
Мониторинг потерь и величин градиентов: Построение графика потерь и мониторинг статистики градиентов позволяют определить, слишком ли высока или низка скорость обучения. Это позволяет легко использовать такие инструменты, как ранняя остановка, чтобы предотвратить переобучение.
В этом разделе мы обсудили некоторые проблемы, связанные с функцией ReLU, и способы их решения.
В этом руководстве мы подробно рассмотрели rectified linear unit, или ReLU. Сначала мы изучили, как работает функция и что делает её уникальной по сравнению с другими функциями активации. Мы также рассмотрели, как можно реализовать эту функцию на Python с использованием NumPy и PyTorch. Затем мы изучили некоторые преимущества и недостатки функции. Наконец, мы также рассмотрели некоторые альтернативы этой функции и преимущества, которые они предлагают.
Чтобы узнать больше о том, как использовать ReLU в PyTorch, ознакомьтесь с .
