Мультиколлинеарность и коэффициент инфляции дисперсии (VIF) в регрессионной модели (с кодом Python)

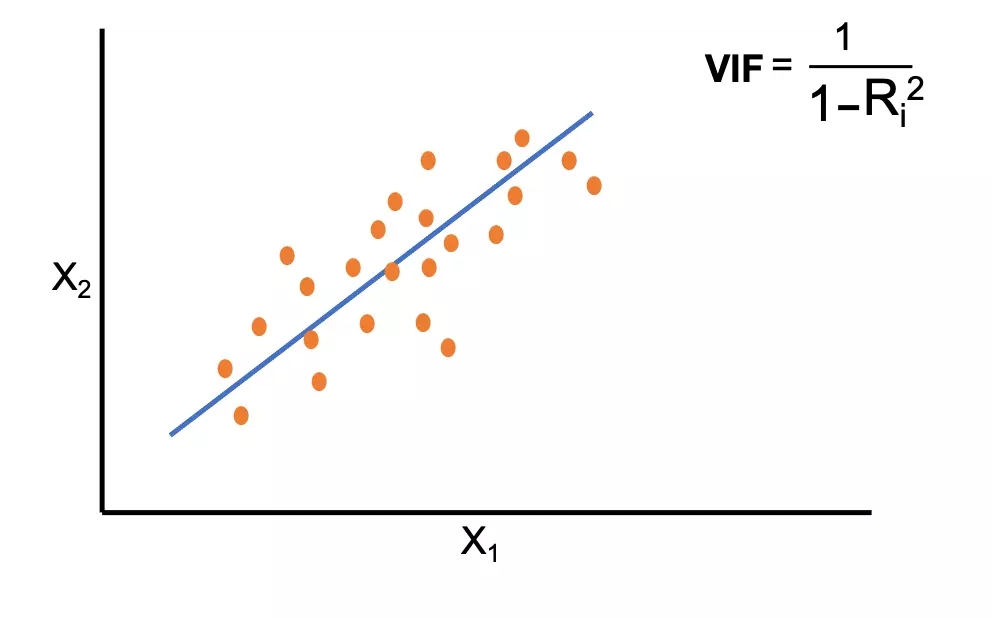
• Мультиколлинеарность и коэффициент инфляции дисперсии (VIF)

• Диагностика мультиколлинеарности с использованием коэффициента инфляции дисперсии (VIF)

• Почему мультиколлинеарность проблематична в регрессионном анализе?

• Как исправить мультиколлинеарность?

• Пример диагностики и коррекции мультиколлинеарности

• Рекомендации

Фактор инфляции мультиколлинеарности и дисперсии (VIF)

Мультиколлинеарность и коэффициент инфляции дисперсии (VIF)

• Мультиколлинеарность относится к высокой корреляции между более чем двумя независимыми переменными в модели регрессии (например, Множественная линейная регрессия). Аналогично, коллинеарность относится к высокой корреляции между двумя независимыми переменными.
• Мультиколлинеарность может возникать из-за плохо спланированных экспериментов (мультиколлинеарность, основанная на данных) или из-за создания новых независимых переменных, связанных с существующими (структурная мультиколлинеарность).

• Коэффициент инфляции дисперсии (VIF) измеряет степень мультиколлинеарности или коллинеарности в регрессионной модели.

Диагностика мультиколлинеарности с использованием коэффициента инфляции дисперсии (VIF)

• VIF (Индекс дополнительной дисперсии), индексы толерантности (ТИ) и коэффициенты корреляции являются полезными метриками для определения мультиколлинеарности.

• Диапазон VIF для оценки мультиколлинеарности задается как,

VIF value	Диагностика
1	Полное отсутствие мультиколлинеарности
1-2	Отсутствие сильной мультиколлинеарности
> 2	Наличие умеренной и сильной мультиколлинеарности.

Примечание: Универсального согласия относительно значений VIF для обнаружения мультиколлинеарности не существует. VIF > 5 или VIF > 10 указывает на сильную мультиколлинеарность, но VIF < 5 также указывает на мультиколлинеарность. Рекомендуется иметь VIF < 2.

• VIF может обнаружить мультиколлинеарность, но не может определить независимые переменные, вызывающие мультиколлинеарность. Здесь анализ корреляции полезен для выявления сильно коррелированных независимых переменных.

Почему мультиколлинеарность проблематична в регрессионном анализе?

• Эффективность регрессионного анализа в значительной степени зависит от структуры корреляции независимых переменных. Мультиколлинеарность вызывает неточности в результатах регрессионного анализа.

• Если в регрессионной модели присутствует мультиколлинеарность, это приводит к смещенной и нестабильной оценке коэффициентов регрессии, увеличивает дисперсию и стандартную ошибку коэффициентов, а также уменьшает статистическую мощность.

• Например, если корреляция между двумя независимыми переменными превышает 0.9, это может значительно изменить коэффициенты регрессии. Иногда также может происходить изменение алгебраического знака коэффициентов регрессии.

• Мультиколлинеарность пропорциональна оценке коэффициентов регрессии. Чем выше корреляция между независимыми переменными, тем больше будет изменение коэффициентов регрессии.

Как исправить мультиколлинеарность?

• Увеличьте размер выборки

• Удалите сильно коррелированные независимые переменные. Если две независимые переменные сильно коррелируют, рассмотрите возможность удаления одной из переменных. Удаление независимых переменных, вызывающих мультиколлинеарность, не приводит к потере информации.

• Объедините сильно коррелированные независимые переменные

Пример диагностики и коррекции мультиколлинеарности

• Теперь вы знаете, что мультиколлинеарность является серьезной проблемой в регрессионных моделях. Здесь мы обсудим пример множественного регрессионного анализа для расчета VIF, используя данные о артериальном давлении.

import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor 
df = pd.read_csv("https://reneshbedre.github.io/assets/posts/reg/bp.csv")
X = df[['Age', 'Weight', 'BSA', 'Dur', 'Pulse', 'Stress']]   # independent variables
y = df['BP']   # dependent variables
X = sm.add_constant(X)
# fit the regression model
reg = sm.OLS(y, X).fit()
# get Variance Inflation Factor (VIF) 
pd.DataFrame({'variables':X.columns[1:], 'VIF':[variance_inflation_factor(X.values, i+1) for i in range(len(X.columns[1:]))]})
  variables       VIF
0       Age  1.762807
1    Weight  8.417035
2       BSA  5.328751
3       Dur  1.237309
4     Pulse  4.413575
5    Stress  1.834845

• В приведенном выше примере независимые переменные вес, площадь поверхности тела (BSA) и пульс (VIF > 2) сильно коррелируют с некоторыми независимыми переменными в модели.

• Поскольку VIF (Variance Inflation Factor) не указывает, какая пара независимых переменных коррелирует, вы можете провести анализ корреляции, чтобы узнать, какие переменные сильно коррелируют.

X = df[['Age', 'Weight', 'BSA', 'Dur', 'Pulse', 'Stress']]   # independent variables
# correlation analysis
X.corr()
# output
             Age    Weight       BSA       Dur     Pulse    Stress
Age     1.000000  0.407349  0.378455  0.343792  0.618764  0.368224
Weight  0.407349  1.000000  0.875305  0.200650  0.659340  0.034355
BSA     0.378455  0.875305  1.000000  0.130540  0.464819  0.018446
Dur     0.343792  0.200650  0.130540  1.000000  0.401514  0.311640
Pulse   0.618764  0.659340  0.464819  0.401514  1.000000  0.506310
Stress  0.368224  0.034355  0.018446  0.311640  0.506310  1.000000

На основании парного корреляционного анализа переменная Weight сильно коррелирует с BSA (r > 0.8) и Pulse (r > 0.6). Для устранения мультиколлинеарности необходимо исключить переменные BSA и Pulse и повторно проанализировать регрессионную модель.

X = df[['Age', 'Weight', 'Dur', 'Stress']]   # independent variables
y = df['BP']   # dependent variables
X = sm.add_constant(X)
# Variance Inflation Factor (VIF) 
pd.DataFrame({'variables':X.columns[1:], 'VIF':[variance_inflation_factor(X.values, i+1) for i in range(len(X.columns[1:]))]})  variables       VIF
0       Age  1.468245
1    Weight  1.234653
2       Dur  1.200060
3    Stress  1.241117

• В обновленной модели отсутствует сильная мультиколлинеарность среди независимых переменных. Эти четыре переменные могут быть использованы в регрессионном анализе.

• Смотрите здесь другой пример использования анализа логистической регрессии для отбора признаков путем диагностики мультиколлинеарности.

Рекомендации

1. Yoo W, Mayberry R, Bae S, Singh K, He QP, Lillard Jr JW. Исследование эффектов мультиколлинеарности в многомерном анализе. Международный журнал прикладной науки и технологии. 2014 Окт;4(5):9.
2. Vatcheva KP, Lee M, McCormick JB, Rahbar MH. Мультиколлинеарность в регрессионных анализах, проведенных в эпидемиологических исследованиях. Эпидемиология (Sunnyvale, Calif.). 2016 Апр;6(2).
3. Kim JH. Мультиколлинеарность и вводящие в заблуждение статистические результаты. Корейский журнал анестезиологии. 2019 Дек;72(6):558.

4. Daoud JI. Мультиколлинеарность и регрессионный анализ. В сборнике: Журнал Физики: Серия конференций 2017 года 1 декабря (Том. 949, № 1, стр. 012009). IOP Publishing.
5. Marcoulides KM, Raykov T. Оценка коэффициентов инфляции дисперсии в регрессионных моделях с использованием методов моделирования скрытых переменных. Измерения в образовании и психологии. 2019 Окт;79(5):874

6. Обнаружение мультиколлинеарности с использованием коэффициентов инфляции дисперсии

Если у вас есть вопросы, комментарии или рекомендации, пожалуйста, напишите мне на [e-mail]

Эта работа распространяется по лицензии Creative Commons Attribution 4.0 International License