Урок 6: Будущие регрессоры
import pandas as pd
# Загрузка набора данных для учебного пособия 4 с дополнительным столбцом температуры
df = pd.read_csv("https://github.com/ourownstory/neuralprophet-data/raw/main/kaggle-energy/datasets/tutorial04.csv")
df.head()
ds
y
temperature
fig = df.plot(x="ds", y=["y", "temperature"], figsize=(10, 6))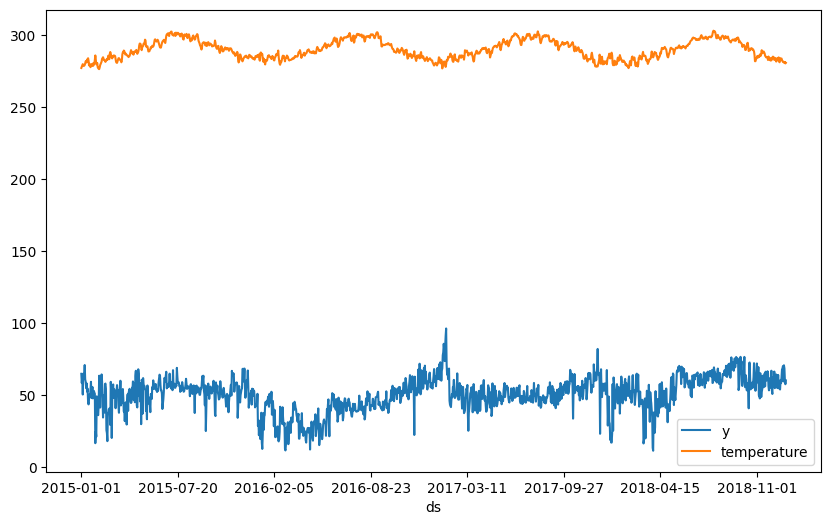
MAE
RMSE
Loss
RegLoss
epoch
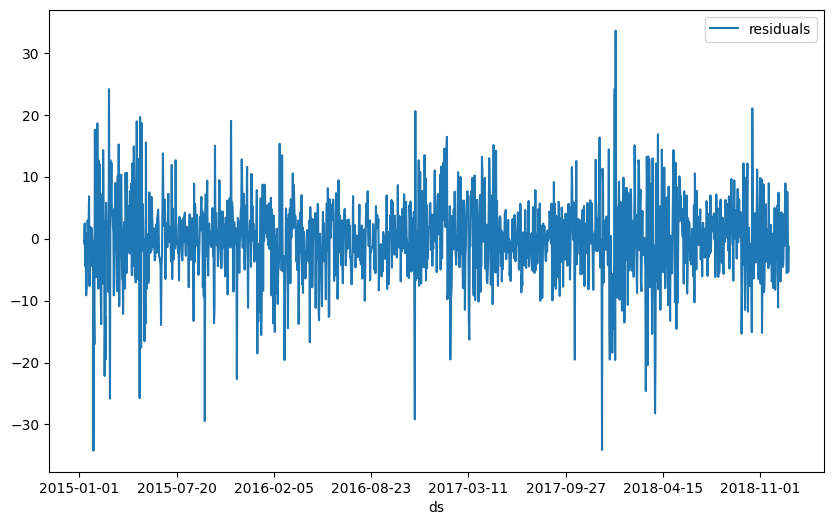
Last updated